Methods

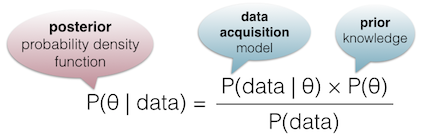
Bayesian Inference

A model describing data formation (e.g. sensor geometry and noise) is combined with all available knowledge about the quantity of interest (e.g. surface roughness). The goal is to compute the posterior probability density function, using Bayes’ rule below. This optimally combines data sources and expert knowledge in a consistent way.

As we are only interested in specific quantities, all others appearing in the models are integrated out – that may involve tricky math and algorithms, but it’s our job!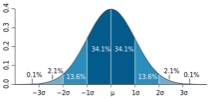

A probability density function encodes both the optimal solution and the uncertainty.
Gaussian approximations allow to simply represent this uncertainty using confidence intervals, and summarize it by the standard deviation.

Probabilistic modeling

Surface reconstruction or elevation model generation may produce noisy results without proper models. Our probabilistic modeling incorporates knowledge about object properties (parameters are estimated automatically if necessary). It helps produce consistent results in low-density areas, or missing data cases.

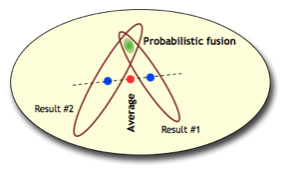
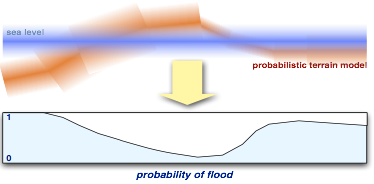
Optimal data fusion

Using carefully designed data formation models, and rigorously propagating uncertainty, allows us to combine data in an optimal way. For instance, multiple LiDAR swaths are fused using objective weights for each point, avoiding arbitrary cutoff angles.

Probabilistic representation of topography

A spatial distribution of uncertainty on topographic models enables the user to obtain consistent results when deriving physical quantities, e.g. for flood analysis or change detection. Global error measures (such as empirical RMS errors) provide an inadequate description of uncertainty, as data density and quality varies spatially.